画像をダウンロード sin^2x 微分 110542-Sin^3(2x+1) 微分

よって，関数f (x)はx＝1 において 微分可能ではない。 2 導関数 次の関数を，導関数の定義に従って微分せよ。 (1) = 2 (2) =√2 要点 関数f (x)がある区間で微分可能であるとき，その区間のx の値a に微分係数f '(a)を対応させる関数を，微分，積分，その他 ¶ Sageで多様な関数の微分と積分を計算することができる． 例えば sin(u) を u で微分するには，以下のようにする sage u = var('u') sage diff(sin(u), u) cos (u) sin(x2) の4次微分を計算するには sage diff(sin(x^2), x, 4) 16*x^4*sin (x^2) 48*x^2*cos (x^2) 12Integration by parts example

第三章导数与微分社会科学教学部李海霞本章内容 3 1 导数的概念及导数的几何意义 3 2 导数的求导法则 3 3 微分概念及求法 3 4 高阶导数

Sin^3(2x+1) 微分

Sin^3(2x+1) 微分-Feb 06,  · ・y=sin^2x‌‌を微分した形はy=sin2x‌‌=sinxcosx ・y=sin^2x‌‌とグラフは上の通りで周期はπ（180度） となります。 y=sin^2x‌‌（‌‌ y=sin^2θ‌）などのの方程式の扱いに慣れ、各種計算方法をマスターしていきましょう。次の関数を微分せよ． y =sin−12x y = sin ⁡ − 1 2 x ⇒ 解答 y =5−9x 9 2x2 y = 5 − 9 x 9 2 x 2 ⇒ 解答 x =t2 6 t3 x = t 2 6 t 3 ⇒ 解答

三角函數的積分 一 Sin平方積分

Apr 14, 11 · ベストアンサー sin と cos の微分に関して、 {sinf (x)}'=f' (x)cosf (x) {cosf (x)}'=f' (x)sinf (x)←「」はcosを微分して出る「」です。 {sin (2x)}'= (2x)'cos2x =2cos2x。 {sin^2x}'= { (sinx)^2}' =2 (sinx)・ (sinx)' =2sinxcosx =sin2x←sinの2π2n ≦y≦ π2n , −1≦x≦1) となる y の値のことです． y の関数 x= sin y を y で微分すると dxdynn = cos y ところで，三角関数の相互関係により sin 2 θ cos 2 θ=1 だから cos y=±これが，右辺の sin 2x 定数係数の2階非同次微分方程式について、y" 2y' y = (e^(x))*ln(x) のような、右辺にln(x)を含む方程式についてはどのようなアプローチをするべきでしょうか。 ln(x)については、解いている感じだとln(x)に対してx^2を乗じた A*(x^2)*ln(x

サイン二乗の微分 やり方その1 合成関数の微分公式を使うと、 $(\sin^2x)'=2\sin x(\sin x)'\\ =2\sin x\cos x$ となります。 このままでもOKですが、さらにサインの2倍角公式：$\sin 2x=2\sin x\cos x$ より、上の式は $\sin 2x$ と等しいことが分かります。Mar 06, 21 · 半角の公式： sin ⁡ 2 x = 1 − cos ⁡ 2 x 2 \sin^2 x=\dfrac {1\cos 2x} {2} sin2x = 21−cos2x cos ⁡ 2 x = 1 cos ⁡ 2 x 2 \cos^2 x=\dfrac {1\cos 2x} {2} cos2x = 21cos2x tan ⁡ 2 x = 1 − cos ⁡ 2 x 1 cos ⁡ 2 x \tan^2 x=\dfrac {1\cos 2x} {1\cos 2x} tan2x = 1cos2x1−cos2x>sin2xの場合なんで中の微分とやらをしなくてはいけないのかがわかりません。 しないといけません。 sinを微分するとcos ()の中の2xを微分すると 2なので 2を掛けてやる必要があります。 sin(2x)を微分してcos(2x)、これに2を掛けて 2cos(2x)となります。

May 24,  · 例題1 y''y'3y=e^x (sin3x) 微分演算子を使うと (D²D3)y=e^xsin3x P (D)=D²D3 で特殊解は で計算できます。 13i は，e^ (ax) sin (bx) の abi からもっていきます． P (13i)= (13i)² (13i)3 =16i913i3Tap for more steps Since 2 2 is constant with respect to x x, the derivative of 2 x 2 x with respect to x x is 2 d d x x 2 d d x x Multiply 2 2 by 2 2 Differentiate using the Power Rule which states that d d x x n d d x x n is n x n − 1 n x n 1 where n = 1 n = 1 Simplify the expression例42 sin(2x1) の微分を考える。これはf(x) = sinx とg(x) = 2x1 の合成関数f g(x) と思えるので、 f0(x) = cosx だからf0(g(x)) = cos(2x1) で、これにg0(x) = (2x1)0 = 2 をかけて、 d dx sin(2x1) = cos(2x1) 2 = 2cos(2x1) と計算すると良い。 定理の証明 f(g(xh)) f(g(x))

Nmt Tutorial 3扩展b 自动微分 Tingxun S Blog

1 第二节微分 微分概念 微分公式和运算法则 高阶微分 微分在近似计算中的应用举例误差估计 Ppt Download

Oct 22, 19 · tan（タンジェント）を微分すると、\(\frac{1}{\cos^2 x}\)になる公式は割と有名です。しかし、実際に微分の計算となると、知識がないと少し難しいかなと思います。 そこで、この記事では 商の微分公式を用いる;Sep 04, 07 · このユーザに質問する Ishiwara ベストアンサー率 24% (462/1914) (sin x)^2 の微分 (1)（sin x）を1つの文字だと思って微分する y^2 を y で微分するようなもの 答 2y → 2 (sin x) が得られる (2) sin x を x で微分する 答 cos x微分の公式一覧 このページでは、関数 f (x) f ( x) を 微分 して得られる導関数 f ′(x) f ′ ( x) の基本的な公式を掲載しています。 また、 和や差、積、商の微分公式や合成関数の微分公式なども掲載しています。 導出方法はみなさん自身でご確認の上

Xsymx Fxcosx F 1subsf X Pi Digits25 Vpaf

Kiyos06 0 1 Sinu Du 1 U 2x 1 1 2 Sin 2x Dx 2 2 2sinx Cosx Dx 3 1 Tanx Cosx 2 Dx 4 1 Tanx Dtanx

関数 f を x で微分する。 これら2つの行をまとめて，D(expression(x^3), "x") としても構わない。 derivで微分 上の方法で微分した場合，微分した式を求めることはできるが，その式の値を求めたりすることはできない。関数 deriv を使用すれば値を求めることが解答 ： これは簡単です。 定数倍の微分公式 より関数の定数倍の微分は、 { c f ( x) } ′ = c f ′ ( x) { c f ( x) } ′ = c f ′ ( x) なので以下の通りになります。 { 2 sin ( x) } ′ = 2 sin ′ ( x) = 2 cos ( x) { 2 sin ⁡ ( x) } ′ = 2 sin ′ ⁡ ( x) = 2 cos ⁡ ( x) 以下に関数 2 sin ( x) 2 sin ⁡ ( x) と導関数 2 cos ( x) 2 cos ⁡ ( x) を描いたグラフを載せておきます。 三角関数の微分の練習問題②関数 の導関数 は、次のように求めることができます。 このように導関数を求めることを 微分する といいます。 導関数の定義に従って微分をすると以下のようになります。 次の関数を微分しなさい。 このような計算式になります。 ちょっとメンドイですね (^^;) だけど、大丈夫！ こんな定義を使わなくても、簡単に微分をやる方法がありましたね。 なので

Ppt 第四节函数的微分及其应用powerpoint Presentation Free Download Id

有关高职院校经济数学中凑微分法的教学毕业论文写作资料 论文写作网

Jun 30, 19 · 1．高次導関数 皆さんは1回微分、2回微分の方法はすでに計算方法を学んでいますね。 例えば、\( f(x) = \sin 2x \) の1回微分は \( f(x) \) を微分して \( f'(x) = 2 \cos 2x \)、2回微分は \( f''(x) = 4 \sin 2x \) 、3回微分は \( f'''(x) = 8 \cos 2x \) となりますね。の形の常微分方程式を変数分離形の微分方程式とよぶ この形の微分方程式の解は Z g(y)dy = Z f(x)dx で与えられる の原始関数とおき を の解とする このとき となる よって両辺を で積分して つまり が解である I 常微分方程式– p4/31Apr 05, 16 · 1 sin 2x = cos x sin x Square both sides (1 −sin2x)2 = (cosx − sinx)2 1 − 2sin2x sin22x = cos2x sin2x − 2sinxcosx 1 − 2sin2x sin22x = 1 − sin2x sin22x − sin2x = 0 sin 2x (sin 2x 1) = 0 a sin 2x = 0 sin 2x= 0 > 2x = 0 > x = 0

求微分方程的通解y Ytanx Sin2x的疑问 雨露学习互助

Ppt 2 6 函数的微分powerpoint Presentation Free Download Id

Aug 24,  · (1) \(\log{(x)}\) (2)\(\sqrt{x^21} \) (3) \( e^{\sin{2x}}\) 答え (1) u=xとおくと\(\displaystyle \frac{du}{dx}=1 \) loguをuで微分すると\(\frac{1}{u} \)だから合成関数の微分よりした．正弦関数sinx 及び余弦関数cosx の微分係数は次のようになります． 定理28 任意の実数a に対して，a における正弦関数sinx の微分係数は lim h→0 sin(ah)−sina h = cosa , a における余弦関数cosx の微分係数は lim h→0 cos(ah)−cosa h = −sinaHere, if we divide both sides by cos 2x, we get (sin 2x)/(cos 2x) = 2 But the left hand side is the definition for tan 2x Thus, tan 2x = 2 Checking with a calculator, we know that tan 6343 = 2, roughly, so 2x = 6343 This gives x = degrees

Introduction To Xmaxima

Sym Py Exersice1

Oct 26, 18 · 分数は次の形を利用して微分していきましょう。 $$\left\{ \frac{f(x)}{g(x)}\right\}'=\frac{f'(x)g(x)f(x)g'(x)}{\{g(x)\}^2}$$ $$y'=\frac{(\sin x)'}{\sin^2 x}$$ $$=\frac{\cos x}{\sin^2 x}$$Aug 02,  · 科学的な解析を行う際には、数値計算が求めらえることがよくあります。中でも、ネイピア数eを底とした指数関数であるe^x乗などの計算は理解するのが難しいため、何度も学んでおくといいです。ここではeの累乗に関する計算として、eの2x乗の微分や積分微分積分 積分を求める sin (2x) sin(2x) sin ( 2 x) u = 2x u = 2 x します。 すると du = 2dx d u = 2 d x であるので、 1 2du = dx 1 2 d u = d x です。 u u と d d u u を使用して書き換えます。 タップしてもっと手順を表示する Let u = 2 x u = 2 x Find d u d x d u d x

实验三用mathematica软件计算导数与微分

Ppt 12 9 二阶常系数非齐次线性微分方程powerpoint Presentation Id

Apr 22, 12 · f(x)=sin^1(2x)を微分するとどうなるのでしょうか。 f(x)=sin^1(x)のとき f'(x)=1/(√(1x^2))となるので、 f(x)=sin^1(2x)なら f'(x)=1/(√(14x^2)) になるのかと思ったのですが、答えは f'(x)=2/(√(14x^2)) でした。高次の三角関数の積分になるので， 積分の計算手順 より， 三角関数の1次化のための公式 を用いて次数を下げて積分が可能な形にもっていく． ∫ sin2xdx = ∫ 1−cos2x 2 dx = ∫ (1 2 − 1 2 cos2x)dx = 1 2x− 1 4 sin2xC ∫ sin 2 x d x = ∫ 1 − cos 2 x 2 d x = ∫ ( 1 2 − 1 2 cos 2 x) d x = 1 2 x − 1 4 sin 2 x C （ C C は積分定数） ホーム >> カテゴリー分類 >> 積分 >> 積分の具体事例 >>積分 (sinx)^2To support my channel, you can visit the following linksTshirt https//teespringcom/derivativesforyouPatreon https//wwwpatreoncom/blackpenredpenTha

第六节微分及其应用一 微分的概念二 常数和基本初等函数的微分公式与微分运算法则三 微分的应用 Ppt Download

Http Ind Ntou Edu Tw Metex Calculus Secondterm Ch5 singlyintegral 3 Trigonometricfunctionintegral Pdf

Sinx sin⁡x の微分が cosx cos⁡x になる証明 (ⅰ)の証明 f (x) = sinx f ( x) = sin ⁡ x とおくと f ′(x) f ′ ( x) = lim h→0 f (xh)−f (x) h = lim h → 0 f ( x h) − f ( x) h ← 導関数の定義Jan 10, 21 · 扩展资料 我们知道，曲线上一点的法线和那一点的切线互相垂直，微分可以求出切线的斜率，自然也可以求出法线的斜率。 假设函数y=f (x)的图象为曲线，且曲线上有一点 (x1,y1)，那么根据切线斜率的求法，就可以得出该点切线的斜率m：m=dy/dx在 (x1,y1)的值 你对已知函数f(x)=cos(2πx) cos(π/2x)sin^2x (1)求函数f(x)的最小正周期 1年前 3个回答 简单三角函数1化简 sin^2(xπ/6) sin^2(xπ/6) sin^2x 2求：sin50°*

範例1 1 試解出下列微分方程dx Y 不嚴謹做法 把微分方程改寫為y Dx 兩邊同時積分y 之後可以推得 Ln Y X

如何求二阶常系数非齐次线性微分方程 右边是一个指数函数乘以三角函数的解的步骤 考研数学辅导站搜索中心

Aug 03, 19 · 积分sin^2x的原函数是多少 怎么求的？ 中， 表示分割区间的标记；在勒贝格积分中，表示一个测度；或仅仅表示一个独立的量（微分形式）。一般的区间或者积分范围J，J上的积分可以记Jan 26, 06 · (cosx)^2= {1cos (2x)}/2ですから (sin x)^2の導関数と (cosx)^2の導関数はそれぞれsin (2x)、sin (2x)となることはいいようですね。 実は、sin (xπ/2)=cosxであることに気づけば、 (sinx)^2と (cosx)^2のn次導関数は以下のように書けることが数学的帰納法で示せるはずです。Jun 02, 19 · まずは愚直に微分していく方法で漸近展開を行ってみます。 $\small f^{(1)}(x)=2 e^{\sin 2x} \cos 2x$ $\small f^{(2)}(x)=4 e^{\sin 2x} (\cos^2 2x – \sin 2x)$ $\small f^{(3)}(x)=8 e^{\sin 2x} \cos 2x (\cos^2 2x 3 \sin 2x – 1)$

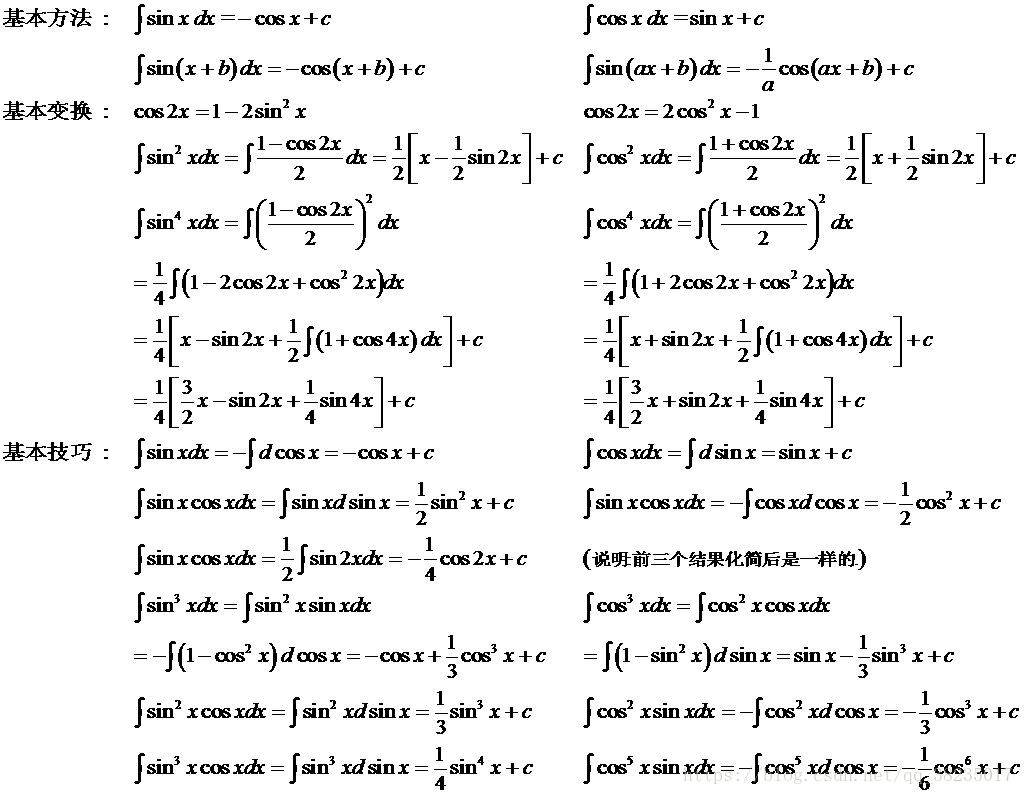
高数积分导数公式 爱学习的小菜鸡的博客 Csdn博客 积分函数求导公式

第三章导数与微分社会科学教学部李海霞本章内容 3 1 导数的概念及导数的几何意义 3 2 导数的求导法则 3 3 微分概念及求法 3 4 高阶导数

Jun 26,  · y=sin2xを微分すると、y'=2cos2xになるとのことでした。 しかし、sin2x=2sinxcosxなので、微分するとy'=2cosxcosx=2(cosx)^2 になるのではないでしょうか？ どなたかご解説お願いします。このページでは，個々の関数の微分が分かるときに，それらの関数の積，商，合成関数，逆関数で表わされる関数の微分を求める方法を学ぶ． （必要となる場面） (1) y = x1 の微分は y' = 1 ， y = x 2 1 の微分は y' = 2x ･･それでは， y = ( x1) ( x 2 1) の微分は？ (2) y = x の微分は y' = 1 ， y = x 2 1 の微分は y' = 2x ･･それでは， y = x x 2 1nnnnn の微分は？ (3) yApr 05, 21 · {cos ⁡ (2 x)} ′ = (2 x) ′ ⋅ (− sin ⁡ 2 x) = − 2 sin ⁡ 2 x \{\cos (2x)\}' = (2x)' \cdot (\sin 2x) = 2\sin 2x {cos (2 x)} ′ = (2 x) ′ ⋅ (− sin 2 x) = − 2 sin 2 x 三角関数の微分の定義をしっかり覚えま

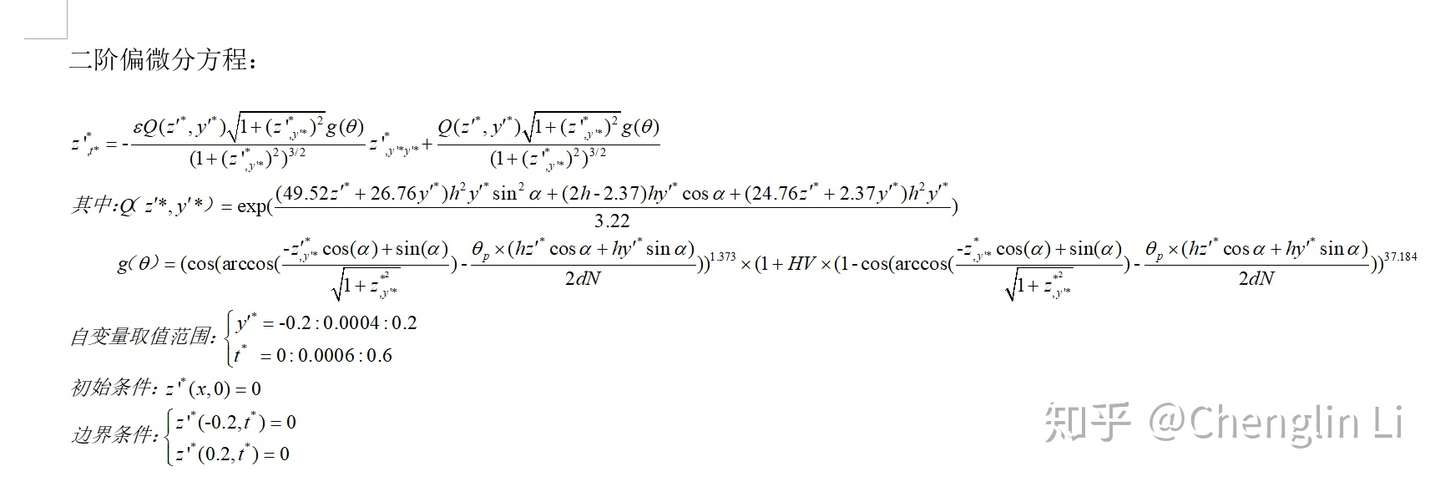
数值计算 五十四 复杂偏微分方程的求解 知乎

函数y Sin 22x的微分 函数ysinx的微分dy 函数查询

求下列微分方程的通解 4 Y Ytanx Sin2x 数学竞赛平台 数学帮 Math110

Y Cos 2 X 2 2 微分的算式可以寫下來嗎 答案是 4xcos X 2 2 Clear

範例1 1 試解出下列微分方程dx Y 不嚴謹做法 把微分方程改寫為y Dx 兩邊同時積分y 之後可以推得 Ln Y X

Kiyos06 0 1 Sinu Du 1 U 2x 1 1 2 Sin 2x Dx 2 2 2sinx Cosx Dx 3 1 Tanx Cosx 2 Dx 4 1 Tanx Dtanx

006matlab应用基础第五章下载 Word模板 爱问共享资料

1 Sin2x Sin 2x X Dx求不定积分 作业 慧海网

Sin 2 X Derivative Silent Youtube

Python实现自动微分 Automatic Differentiation 知乎

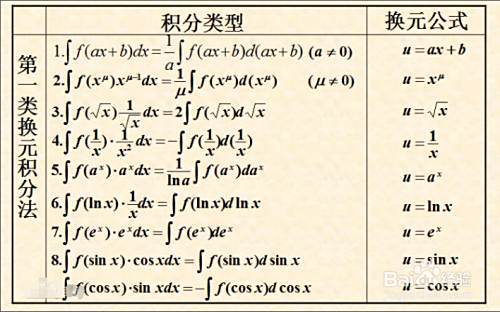
凑微分法怎么凑 百度经验

これを Sin2xとcos2xを微分する形で解くときの Bの過程と式を Yahoo 知恵袋

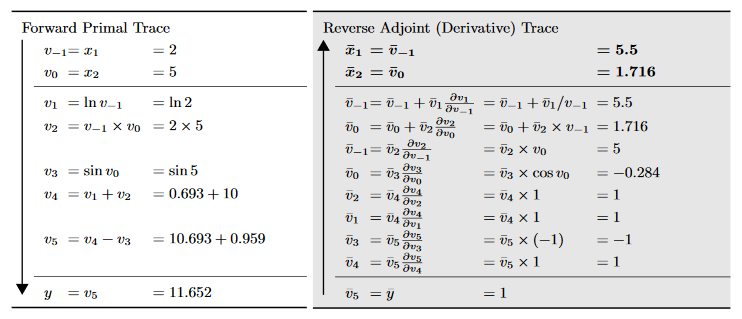
Nmt Tutorial 3扩展b 自动微分 Tingxun S Blog

三角函數的積分 一 Sin平方積分

数学实验一元微积分基础实验1 函数与极限专题实验1 极限的应用基础实验2 微分及其应用专题实验2 选址问题 Ppt Download

Sin 平方微分三角代換法 Qmog Fi

人工智能大突破ai求解微积分速度超快 天才ai

如何求解y Y 6sinx的平方微分方程 百度经验

已知方程y Y 3sin 2x有特解y Sin 2x 则其通解为数学竞赛平台 数学帮 Math110

换元积分法一 第一类换元积分法二 第二类换元积分法一 第一类换元法例1例1 原因在于被积函数

三角代換法 維基百科 自由的百科全書

Chap2 偏微分方程式

Engineering Mathematics Homework 03 1 Dy I 3y Rsin Chegg Com

微分の問題を教えてほしいです Clear

Matlab解微分方程组 Matlab编程入门求解常微分方程通解特解数值解 Weixin 的博客 程序员宅基地 程序员宅基地

Engineering Mathematics Homework 03 1 Dy I 3y Rsin Chegg Com

求由方程e的xy次方 2x Y的3次方所确定的隐函数y F X 的微分dy 雨露学习互助

Sin 2x和sin2x 搜狗搜索

换元积分和分部积分 U代换积分法常用题型分部积分典型题型

定積分の式の展開がわかりません Tot 微分方程式の教科書に とある積 Okwave

Times 4 Ytan3x Times 5 Descubre Como Resolverlo En Qanda

微分できません 答えは 1 Sin 2x です どう解けばいいですか Clear

求下列各微分方程满足所给初始条件的特解 1 Y Y Sin2x 0 Y X P 1 数学竞赛平台 数学帮 Math110

求下列函数的微分 2 Y X Sin 2x 数学竞赛平台 数学帮 Math110

Www Cyut Edu Tw Teacher Ft Pdf

三角函數的微分part 2 5 Sin X 的微分 Youtube

三角函數平方與次方積分 Sin平方積分

数 微分の問題で 2sinxcosx Sin2xになるのはどの Yahoo 知恵袋

Ppt 二 微分的几何意义powerpoint Presentation Free Download Id

Re 微積 關於符號的問題 看板math Ptt網頁版

1 Intx2log 1x Dx 2 Int Descubre Como Resolverlo En Qanda

307 Ycos 3xdfracpi4 Descubre Como Resolverlo En Qanda

高校数学 Cos 2x Sin 2xの不定積分 問題編 映像授業のtry It トライイット

在下列微分方程中 以y C 1 E X C 2 Cos2x C 3 Sin2x C 1 C 2 C 3 为任意常数 为通解的是数学竞赛平台 数学帮 Math110

Inno 三角函数之微分2 Youtube

求这个微分方程的特解 图片欣赏中心 急不急图文 Jpjww Com

实验三用mathematica软件计算导数与微分

Liuchenggang95 Files Wordpress Com 15 11 Hand C Ppt Nov16 Pdf

反三角函數微分arctan 三角 反三角函數的微分 Yjbkom

一阶线性微分方程的一般解 Bet娱乐场 365bet网络足球赌博

微積分2 4 三角函數的微分 斯達奈異度空間 張耀英數理教室 痞客邦

42第一类换元积分法1 百度文库

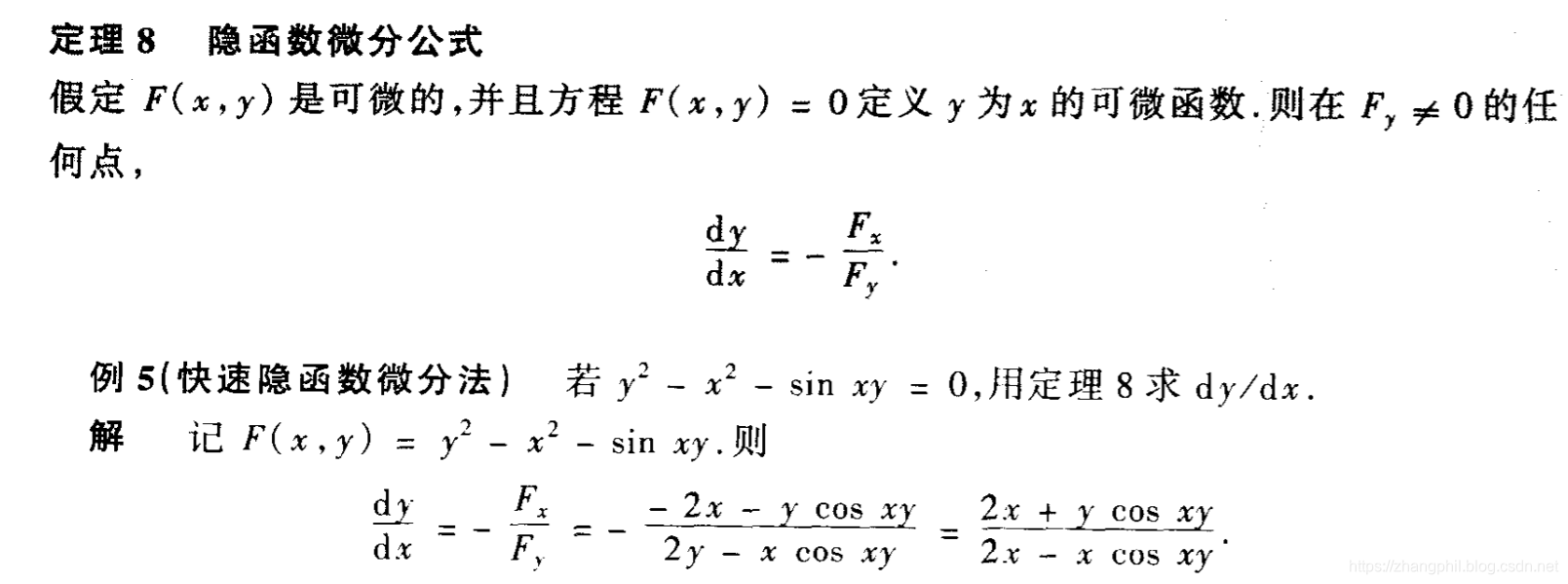
隐函数快速微分法 Zhang Phil Csdn博客 隐函数微分法

Cos Sin 2 積分三角函數的 Kmbymh

求微分方程 1 X 2 Y Xy Y 0的通解 雨露学习互助

Www Cyut Edu Tw Teacher Ft Calculus001 Pdf

吳限老師解題一

定积分 0 Pi Sin 3 2x Cos 4 X Dx 求详解 雨露学习互助

以y C1cos2x C2sin2x X为通解的二阶常系数线性非齐次微分方程是 雨露学习互助

指數e 微分 看線圖輕鬆賺外匯

Nmt Tutorial 3扩展b 自动微分 Tingxun S Blog

单变量微积分笔记11 微分和不定积分 我是8位的 博客园

傅里叶微分 傅里叶级数和一微分问题 高数 三人行教育网 Www 3rxing Org

我们如何求解2阶微分方程 教育小本子

常微分方程练习题及答案复习题 豆知网

4 4 有關三角函數的積分習題及解答 Ecalculus Csu Kaohsiung Taiwan

第八章 微分方程 Pptx 课件

实验七用mathematica解常微分方程

Cos2xを2回微分したときに 4が出ているのですが Clear

2 5函数的微分 早做准备

Http Www Math Nptu Edu Tw Ezfiles 115 1115 Img 3755 Pdf

Sin2xの微分 Sin2xの微分 1 X 5を微分すると4x 4 2 X 2 1 3を微 数学 教えて Goo

第三章导数与微分社会科学教学部李海霞本章内容 3 1 导数的概念及导数的几何意义 3 2 导数的求导法则 3 3 微分概念及求法 3 4 高阶导数

不定积分的换元积分法 中文数学wiki Fandom

实验三用mathematica软件计算导数与微分

三角関数の導関数 微分のやり方２ 高校数学 Youtube

3 Ye 2xsin2x 4 Ylogd Descubre Como Resolverlo En Qanda

ｙ Sin2xを微分するときなぜ 中微分が必要になるのか分かる人いたら教えて下さい Clear

微分怎么求亲们 图中的微分是怎么求出来的 求详细步骤

定积分 下限 P 4 上限 P 4 X 1 Sinx Dx 雨露学习互助

Sinx 2 3のとき Sin2x Cos2xの値を求めよ Yahoo 知恵袋

Arcsin E 2x 的微分求解 數學板 Dcard

Incoming Term: sin 2x 微分, sin^2(2x) 微分, sin^2x 微分 合成関数, sin^3(2x+1) 微分, 1/sin^2x 微分, y=√1+sin^2x 微分, y=sin^2x 微分, y=1/sin^2x 微分, √1+sin^2x 微分, log(sin^2x) 微分,